Reto II: Otra vez el oscilador armónico. ¿Por qué no?

En esta ocasión vamos a volver a retomar el tema del oscilador armónico. Dicho tema ha sido expuesto en este blog y las entradas relacionadas están contenidas en los siguientes minicursos:

Teorías clásicas a través del oscilador armónico

De la clásica a la cuántica

En el primer minicurso referenciado hablamos de la teoría clásica del oscilador armónico. En el segundo minicurso hablamos de cómo se cuantiza una teoría física basandonos extensamente en el oscilador armónico.

Aquí vamos a hacer un uso extensivo de la matemática de la cuántica que se puede ver en la primera entrada del minicurso:

Mecánica cuántica

Para finalizar, sería muy muy recomendable que se leyera (y sería excepcional que se hubiera trabajado con lápiz y papel) la entrada:

Reto: ¿Te atreves? Un poco de malabarismo matemático

Esta entrada está dedicada especialmente al amigo osguk.

Un poco de repaso

El oscilador armónico en una dimensión viene determinado por una ecuación de Schrödinger de la siguiente forma:

$\hat{H}\psi_n(x)=E_n\psi_n(x)$

– $\psi_n(x)$ Representa el estado cuántico del oscilador que tiene una energía $E_n$ .

– $\hat{H}$ Representa el observable Hamiltoniano, que es el operador matemático que representa la energía total del sistema cuántico. En este caso el operador tiene la forma:

$\hat{H}=\dfrac{\hat{p}^2}{2m}+\dfrac{1}{2}k\hat{x}^2$

Donde $\hat{p}=i\hbar\dfrac{d}{dx}$ representa el operador momento.

Y $\hat{x}$ (que actúa multiplicando la función de onda por su correspondiente x) representa el operador posición.

Recordemos que la relación fundamental de la cuántica venía dada en términos del conmutador entre las variables elementales del sistema (en este caso posiciones y momentos) y que verifican:

$[\hat{x},\hat{p}]=i\hbar$

Dado que estas variables no conmutan no podemos medirlas a la vez (por el principio de indeterminación de Heisenberg). Eso se traduce en un hecho evidente, las funciones de onda sólo pueden depender o bien de las posiciones (x) o bien de los momentos (p).

Pero la historia no acaba ahí, la cuestión esencial es respetar la estructura del conmutador que acabamos de escribir, así que uno puede encontrar combinaciones de posiciones y momentos que nos den otras variables con las cual describir el oscilador y que dicho conmutador siga siendo válido.

Explicaremos esto con más detalle.

Reescribiendo las variables del oscilador

El Hamiltoniano del oscilador, como hemos visto, es:

$\hat{H}=\dfrac{\hat{p}^2}{2m}+\dfrac{1}{2}k\hat{x}^2$

Recordemos que hay una relación entre la frecuencia de oscilación $\omega$ , la masa de la partícula que oscila $m$ y una característica del oscilador (en caso de ser un muelle la constante elástica del mismo) $k$ . La relación es:

$\omega=\sqrt{\dfrac{k}{m}}$

Por tanto, es fácil ver que el Hamiltoniano se escribe:

$\hat{H}=\dfrac{\hat{p}^2}{2m}+\dfrac{1}{2}m\omega^2\hat{x}^2$

Intentemos factorizar el Hamiltoniano. Para ello vamos a hacer uso de la siguiente identidad de números complejos:

$(a+ib)(a-ib)=a^2+b^2$

Un número complejo tiene la forma $c+ib$ donde $c$ y $b$ son número reales. Y $i=\sqrt{-1}$ y cumple:

– $i^2=ii=-1$

– $i^3=iii=-i$

– $i^4=iiii=1$

Por tanto,

$(c+ib)(c-ib)=c^2+icb-icb-i^2b^2=c^2+b^2$

Siguiendo esta lógica podemos definir las siguientes agrupaciones:

$a=\sqrt{\dfrac{m\omega}{2\hbar}}\left(\hat{x}+\dfrac{i}{m\omega}\hat{p}\right)$

$a^\dagger=\sqrt{\dfrac{m\omega}{2\hbar}}\left(\hat{x}-\dfrac{i}{m\omega}\hat{p}\right)$

Estos serán los objetos básicos con los que vamos a trabajar a partir de ahora. Pero hemos de ser cuidadosos en verificar que cuando trabajemos con ellos el conmutador entre posiciones y momentos mantiene su estructura: $[\hat{x},\hat{p}]=1$ .

Conmutador con los nuevos objetos

Calculemos dicho conmutador: $[a,a^\dagger]$ :

Lo haremos paso a paso:

1.- Empezamos poniendo la expresión entera

$[a,a^\dagger]$

= $[\sqrt{\dfrac{m\omega} {2\hbar}}\left(\hat{x}+\dfrac{i}{m\omega}\hat{p}\right)$ , $\sqrt{\dfrac{m\omega}{2\hbar}}\left(\hat{x}-\dfrac{i}{m\omega}\hat{p}\right)]$

2.- Recordemos que las constantes salen del conmutador: $[nA,mB]=nm[A,B]$ donde n y m son constantes. Por lo tanto queda:

$=\dfrac{m\omega}{2\hbar}[\hat{x}+\dfrac{i}{m\omega}\hat{p}$ , $\hat{x}-\dfrac{i}{m\omega}\hat{p}]$

3.- Ahora aplicando las reglas $[A+B,C]=[A,C]+[B,C]$ y $[A,B+C]=[A,B]+[A,C]$ y el segundo paso cuando sea necesario, obtenemos:

$=\dfrac{m\omega}{2\hbar}\left([\hat{x},\hat{x}]-\dfrac{i}{m\omega}[\hat{x},\hat{p}]+\dfrac{i}{m\omega}[\hat{p},\hat{x}]+\dfrac{1}{m^2\omega^2}[\hat{p},\hat{p}]\right)$

4.- Recordemos que el conmutador de un operador consigo mismo se anula: $[A,A]=0$ . Por tanto:

$=\dfrac{m\omega}{2\hbar}\left(-\dfrac{i}{m\omega}[\hat{x},\hat{p}]+\dfrac{i}{m\omega}[\hat{p},\hat{x}]\right)$

5.- Además sabemos que $[A,B]=-[B,A]$

$=\dfrac{m\omega}{2\hbar}\left(-\dfrac{i}{m\omega}[\hat{x},\hat{p}]-\dfrac{i}{m\omega}[\hat{x},\hat{p}]\right)$

6.- Agrupando:

$=\dfrac{m\omega}{2\hbar}\dfrac{-2i}{m\omega}[\hat{x},\hat{p}]=-\dfrac{i}{\hbar}[\hat{x},\hat{p}]$

7.- Ahora tenemos que imponer que la teoría sea consistente, es decir, que $[\hat{x},\hat{p}]=i\hbar$ eso impone que:

$[a,a^\dagger]=-\dfrac{i}{\hbar}i\hbar=1$

Por lo tanto, si empleamos los nuevos objetos con un conmutador $[a,a^\dagger]=1$ estamos seguros de que $[\hat{x},\hat{p}]=i\hbar$ y la teoría sigue siendo la misma.

En $a$ y $a^\dagger$ tenemos la información de momentos y posiciones, pero de tal forma que se siguen satisfaciendo la indeterminación en los mismos. Dichos objetos tampoco conmutan por lo tanto seguimos teniendo la misma estructura en la teoría.

El Hamiltoniano

Sería muy interesante que comprobarais lo siguiente:

$aa^\dagger=\dfrac{1}{\hbar\omega}\hat{H}+\dfrac{1}{2}$

$a^\dagger a=\dfrac{1}{\hbar\omega}\hat{H}-\dfrac{1}{2}$

En caso de tener problemas para llegar a estas expresiones simplemente comentadlo y las desarrollamos.

Entonces el Hamiltoniano se puede escribir como:

$\hat{H}=\hbar\omega a^\dagger a +\dfrac{\hbar \omega}{2}$

Conclusión de esta entrada

En esta entrada hemos visto como podemos cambiar de objetos básicos de nuestra teoría, siempre con cuidado de mantener sus características inalteradas, en este caso la estructura de conmutadores. Hemos visto como podemos reescribir el Hamiltoniano.

Ahora el reto sería el siguiente:

Partiendo del Reto inicial intentar traducirlo a términos físicos relacionados con el oscilador armónico.

¿Os atrevéis?

Para finalizar diremos que estamos muy cerca de entrar en un tema peliagudo e interesante, la creación y destrucción de partículas. Esta es la base del entendimiento que tenemos de los campos cuánticos. En divulgación nos dicen muchas veces que las partículas asociadas a los campos cuánticos aparecen y desaparecen, ¿podéis ver por donde van los tiros?

Nos seguimos leyendo

8 Respuestas a “Reto II: Otra vez el oscilador armónico. ¿Por qué no?”

Miguel Cámara | 2 octubre, 2015 en 18:57 | Responder

Es excelente tu sección y además permite repasar conceptos de la carrera (que ya fue hace un tiempo). Mucho ánimo y gracias.
Mariona | 30 agosto, 2014 en 14:08 | Responder

Hola,
llevo mucho rato intentando deducir el Hamiltoniano en función de a⁺, a al revés: sustituyendo en H=P²/2m + 1/2mw²X² las expresiones de P y X y no consigo el resultado esperado; siempre me sale que H= hw/2 (a⁺² + a² + a⁺a + 1/2).
En realidad lo necesito para compararlo y encontrar el Hamiltoniano de dos dimensiones: H= P²/2m + 1/2mw²(4X² + Y²) expresado en las componentes a⁺, a en x e y.
Solo que pudieras ayudarme en la primera parte estaría muy muy agradecida porque el miércoles tengo un examen y me preocupa un poco esto 😦
45cr CharlieC | 12 noviembre, 2011 en 0:27 | Responder

En el paso 3.,¿como logra llegar a multiplicar por los operadores x,x , p,x, x.p, y p,p, que no logro llegar partiendo de la fòrmula preestablecida de que A +`B,C.
45cr CharlieC | 11 noviembre, 2011 en 20:00 | Responder

Esto lo habìa visto en Fisica IV, no tan desmenuzado como lo presenta CC, hay cuestiones nuevas aquì, es como para darse banquete con esto, aquì empezamos a utilizar lo aprendido en secciones anteriores, ya entiendo todo el periplo que sorteamos al principio, fue necesario, valiò la pena, esta es una buena herramienta para definirlo todo.
Cuentos Cuánticos | 27 octubre, 2011 en 19:31 | Responder

El Hamiltoniano clásico es:

$H=\dfrac{p^2}{2m}+\dfrac{1}{2}m\omega^2 x^2$

Ahora calcula los productos $a^\dagger a$ y $aa^\dagger$ .
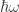Multiplicalos por $\hbar\omega$ y verás que cada uno de ellos te da el Hamiltoniano.

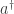Pero ahora tenemos un problema, $a$ y $a^\dagger$ son operadores cuánticos que no conmutan. Entonces tenemos que enfrentarnos a la pregunta ¿Qué ordenación hemos de elegir para representar el Hamiltoniano cuántico $a^\dagger a$ o $aa^\dagger$ ?

La respuesta es que en principio uno no puede preferir una ordenación sobre la otra por tanto elegimos calcular esto:

$\hbar\omega(a^\dagger a+aa^\dagger)$

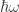y eso tiene que salir $2H$ (el factor $\hbar\omega$ da un poco igual en qué término lo pongas).

Pero ahora decidimos que la ordenación que nos gusta es: $a^\dagger a$ . Por lo tanto en la suma anterior el segundo término lo transformamos en $a^\dagger a$ usando las reglas de conmutación y te tiene que quedar:

$\hbar\omega (2a^\dagger a +1)=2\hat{H}$

A partir de ahí es directo. Si haces lo mismo usando la otra ordenación obtienes el otro resultado.

Si no te sale lo detallamos aún más.

Ánimo….
Edazez | 27 octubre, 2011 en 19:02 | Responder

Podrías detallar cómo llegas a las fórmulas del Hamiltoniano finales?
No logro sacar el sumando 1/2
Gracias!
- Edazez | 27 octubre, 2011 en 19:12 | Responder
  
  Olvídalo. Me he liado yo solo. Gracias.
Pingback: Oscilones | Cuentos Cuánticos