Acción de Polyakov 1

En esta entrada vamos a introducir la acción de Polyakov que es una acción que describe las cuerdas que hemos venido tratando hasta ahora en el curso de Introducción a las supercuerdas.

Para esta entrada hemos empleado apuntes personales y los libros que hemos reflejado en la página mencionada: Introducción a las supercuerdas. Nos consta que hay muchos sitios donde se ha hablado de este tema seguramente mucho mejor que lo que podamos hacer nosotros aquí, por ejemplo:

Polyakov Action

Ni que decir tiene que hemos copiado esta entrada palabra por palabra de aquí: Fuente de la copia palabra por palabra. No lo hemos copiado todo y hemos repetido algunas palabras, algunas posiblemente no aparezcan en la fuente y son invención nuestra.

Esperamos que os resulte interesante la entrada.

La acción de Nambu-Goto de nuevo

En la entrada relativa a la acción de la cuerda clásica llegamos a la acción de Nambu-Goto:

$S=-T\int_{\tau_i}^{\tau_f}d\tau\int_0^l d\sigma\sqrt{-\gamma}$

Pero aquí nos encontramos con una problemática parecida a la acción de la partícula libre relativista que fue discutida aquí: Partícula Relativista 2.

En concreto el que aparezca la raíz cuadrada en la acción siempre es incómodo. Los procedimientos matemáticos son más tediosos y la cuantización de la teoría se complica mucho. Así que el objetivo es encontrar una acción equivalente a la de Nambu-Goto, nos da las mismas ecuaciones de movimiento, y que no contenga una raíz cuadrada.

La acción de Polyakov

Lo que hacemos ahora es emular lo que hicimos en Partícula Relativista 2, es decir, introducimos un campo auxiliar (en este caso una métrica sobre la hoja de mundo que sustiende la cuerda en su evolución en el espaciotiempo) $h_{\alpha\beta}$ que nos ayude a definir una acción que no contenga una raíz cuadrada de los campos físicos de interés (en este caso las coordenadas $X^\mu$ .

La acción de Polyakov es:

$S_P=-\dfrac{T}{2}\int d^2\sigma \sqrt{-h}h^{\alpha\beta}\partial_\alpha X^\mu \partial_\beta X^\nu \eta_{\mu\nu}$

– $h_{\alpha\beta}$ es una métrica en la hoja de mundo de la cuerda. Por tanto sus índices toman valores 0,1.

– $\sqrt{-h}$ es la raíz cuadrada del determinante de la métrica auxiliar cambiado de signo.

– $d\sigma^2=d\tau d\sigma$

– $\eta_{\mu\nu}$ es la métrica en el espaciotiempo que contiene a la cuerda (d dimensional). Sus índices tomarán valores de o a d-1.

Esta acción es la apropiada para iniciar un procedimiento de cuantización consistente. Pero antes de eso hemos de mostrar que es equivalente a la acción de Nambu-Goto. Ese cálculo es muy tedioso, así que lo efectuaremos en la siguiente entrada del curso con todos los detalles necesarios para seguir la lógica del cálculo.

Es muy interesante que se lean las entradas de la partícula relativista de nuevo porque el espíritu de lo que estamos haciendo aquí ya lo mostramos en aquellas entradas pero en un caso más simple.

Nos seguimos leyendo…

5 Respuestas a “Acción de Polyakov 1”

Anónimo | 7 May, 2012 en 19:02 | Responder

dices que es muy tedioso demostrar que son iguales

Si dices $h_{\alpha \beta} = \partial X^u_\alpha \partial X^v_\beta \eta_{uv}$

luego queda que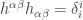 $h^{ \alpha \beta} h_{\alpha \beta} = \delta^i_i$ lo que es 1

y asi me queda la accion de nambu-goto

Estoy casi seguro de que demostrarlo de la forma anterior es incorrecto, pero ¿porque es incorrecto?, por lo menos a mi las matematicas me calzan…

Un saludo
- Cuentos Cuánticos | 7 May, 2012 en 19:39 | Responder
  
  a) Eso no es correcto porque la métrica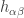 $h_{\alpha \beta}$ es una métrica sobre la hoja de mundo de la cuerda que no tiene porque estar relacionada de forma directa con la métrica inducida sobre dicha hoja de mundo a partir de la métrica en el target.
  
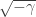  b) Vamos que el problema es relacionar $\sqrt{-h}$ con $\sqrt{-\gamma}$ , donde $-\gamma$ es el determinante cambiado de signo de la métrica inducida.
  
  Los cálculos son tediosos pero no imposible. Trataré de organizar la entrada para pasar de Polyakov a Nambu-Goto en breve para que veas todos los detalles.
  
  Otra cosa es que el producto $h^{\alpha \beta}h_{\alpha \beta}$ no te de uno sino la traza de la métrica.
Carlos Reyes | 2 May, 2012 en 0:47 | Responder

Tiene razòn, ya que màs para alante la cosa se complica un poco màs y esta acciòn, aun introducièndole una mètrica resulta màs simple la cuantizaciòn, nos seguimos leyendo.
Carlos Reyes | 15 abril, 2012 en 23:33 | Responder

Una vez leido y releido Partìcula Relativista 2, se entiende el objeto de su aplicaciòn en la acciòn de Polyakov, ahora, lo que no entiendo es el artificio realizado introduciendo la mètrica para lograr el objetivo, espero que en las pròximas entradas podamos aclarar esto.
- Cuentos Cuánticos | 17 abril, 2012 en 9:27 | Responder
  
  Lo que se hace aquí es simplemente mostrar que hay otra acción que da las mismas ecuaciones de movimiento. A su vez esta acción tiene mejores propiedades que hacen que su cuantización sea más simple. Para llegar a esta nueva forma de la acción, equivalente a la forma natural presentada previamente, hay que introducir una métrica. No tiene más. Si tienes más dudas no dudes en preguntar. Un saludo